25~26高三上·陕西师大附中一模·第14题

$\frac{13}{23}$

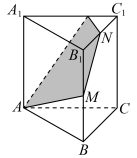
【题目】如图，点$A$，$BB_{1}$的中点$M$及$B_{1}C_{1}$的中点$N$所确定的平面把直三棱柱$ABC – A_{1}B_{1}C_{1}$切割成体积不同的两部分，记小部分的体积为$V_{1}$，大部分的体积为$V_{2}$，则$\frac{V_{1}}{V_{2}} = \underline{\quad\quad}$．

【答案】$\frac{13}{23}$

【解析】设平面$AMN$与棱$A_{1}C_{1}$交点为$D$，则$A_{1}D = 2DC_{1}$，（可先补成四棱柱，如图易得结论）

所以$S_{\triangle DNB_{1}} = \frac{1}{6}S_{\triangle A_{1}B_{1}C_{1}}$，$S_{A_{1}AMB_{1}} = \frac{3}{4}S_{A_{1}ABB_{1}}$，

$\frac{V_{M-DNB_{1}}}{V_{ABC – A_{1}B_{1}C_{1}}} = \frac{\frac{1}{3}S_{\triangle DNB_{1}} \cdot h}{S_{\triangle A_{1}B_{1}C_{1}} \cdot 2h} = \frac{1}{36}$，$\frac{V_{D – A_{1}AMB_{1}}}{V_{ABC – A_{1}B_{1}C_{1}}} = \frac{V_{D – A_{1}AMB_{1}}}{\frac{3}{2}V_{C – A_{1}ABB_{1}}} = \frac{\frac{1}{3}S_{\triangle A_{1}AMB_{1}} \cdot h_{1}}{\frac{1}{2}S_{A_{1}ABB_{1}} \cdot \frac{3}{2}h_{1}} = \frac{1}{3}$，

所以上部分几何体体积$V_{M-DNB_{1}} + V_{D – A_{1}AMB_{1}}$$= \left(\frac{1}{36} + \frac{1}{3}\right)V_{ABC – A_{1}B_{1}C_{1}} = \frac{13}{36}V_{ABC – A_{1}B_{1}C_{1}}$，

因此小部分的体积和大部分的体积之比为$13:(36 – 13) = 13:23$，

故答案为：$\frac{13}{23}$.